This is a short summary of best practices for applying multilayer neural networks to arbitrary supervised learning problems and the capabilities of OpenANN.

Network Architecture

The neural network should be as simple as possible to avoid overfitting. Start with a linear network without hidden layers and only add hidden layers or nodes if it improves the performance of the network. In principle, a neural network with one hidden layer, a nonlinear activation function in the hidden layer and a "sufficient" number of hidden units is able to approximate arbitrary functions with arbitrary precision. In practice, adding more layers can improve the performance of the neural network in terms of time. A few number of hidden nodes is usually not sufficient to fit the training set good enough. However, if the number of hidden nodes is to high, the generalization is not good enough, i.e. the neural net overfits the training data. Tuning the network architecture is not simple.

Types of Layers

A neural network can contain many types of layers. In OpenANN, the multilayer neural network class is called Net. To initialize a Net you have to define its layers which is done by calling member functions of Net. The most important layers are the input layer and the output layer. These are required to specify the input and output dimensions of the network. If there are no hidden layers we are only able to approximate linear functions. To represent more complex functions we can add various types of layers. Here is an incomplete list of available types of hidden layers.

FullyConnected: each neuron is connected to each neuron of the previous layer.
RBM: a restricted boltzmann machine that can be pretrained with unlabeled data.
Compressed: fully connected layer. The I incoming weights of a neuron are represented by M (usually M < I) parameters.
Extreme: fully connected layer with fixed random weights.
Convolutional: consists of a number of 2-dimensional feature maps. Each feature map is connected to each feature map of the previous layer. The activations are computed by applying a parametrizable convolution, i. e. this kind of layer uses weight sharing and sparse connections to reduce the number of weights in comparison to fully connected layers.
Subsampling: these will be used to quickly reduce the number of nodes after a convolution and obtain little translation invarianc. A non-overlapping group of nodes is summed up, multiplied with a weight and added to a learnable bias to obtain the activation of a neuron. This is sometimes called average pooling.
MaxPooling: this is an alternative to subsampling layers and works usually better. Instead of the sum it computes the maximum of a group and has no learnable weights or biases.
LocalResponseNormalization: lateral inhibition of neurons at the same positions in adjacent feature maps.
AlphaBetaFilter: this is a recurrent layer that estimates the position and velocity of the inputs from the noisy observation of the positions. Usually we need this layer for partially observable markov decision processes in reinforcement learning.
Dropout layer: a technique to increase the generalization of a neural network. Neurons are randomly dropped out during training so that they do not rely on each other.

Activation Functions and Error Functions

For regression problems, the error function that should be optimized is the mean sum of squared errors (MSE) and in the output layer the activation function should be linear (LINEAR). For multiclass classification problems, the error function usually should be cross entropy (CE) and the activation function softmax (SOFTMAX, internally SOFTMAX has the same value as LINEAR, the actual activation function depends on the error function, i.e. it is not possible to use softmax activation function in combination with MSE). Thus, the labels have to be represented through 1-of-c encoding, that is to represent C classes C outputs are required. Each output is binary and only one output should be 1, all other outputs have to be 0. The index of the 1 indicates the actual class c. The predictions of the network might not always be 0 or 1. Since the softmax activation function assures that all outputs sum up to 1, we can even interpret the outputs as class probabilities. To obtain the most likely predicted class, we compute the index of the maximum value. However, for two classes, MSE and TANH activation function sometimes work well enough, i.e. we only need one output and devide its range into two regions of (usually) equal size and each region corresponds to one of the two class.

In the hidden layers, nonlinear activation function are required. Available options are:

LOGISTIC
TANH or TANH_SCALED
RECTIFIER

We can distinguish saturating activation functions (sigmoid: LOGISTIC, TANH, TANH_SCALED) and non-saturating activation functions (RECTIFIER). The advantage of sigmoid activation function is that they generate more smooth functions. Their disadvantage is that they do not work very well for deep architectures because they make the error gradient of the first layers very small.

Optimization Algorithm

We can choose between stochastic gradient descent (MBSGD), conjugate gradient (CG), limited storage Broyden-Fletcher-Goldfarb-Shanno (LBFGS) and Levenberg-Marquardt (LMA). LMA is usally the best algorithm because it uses second-order information of the error function, i.e. it approximates the second derivative. But it has some drawbacks:

It works only for MSE.
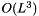It has time complexity , where L is the number of weights.
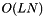It has space complexity , where N is the number of examples.

Thus, it is neither applicable for large nets, nor for large datasets. In this case, we often use MBSGD because it has only 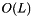$ O(L) $ time and space complexity. It usually works very well for large redundant datasets for classification. It might also be useful to take a look at conjugate gradient for datasets that are not redundant, e.g. regression problems. For networks like auto-encoders, L-BFGS is usually the standard optimization algorithm.

References

More tips can be found in the following documents. They are freely available.

[1] Sarle, W. S.: Neural Network FAQ, postings to the Usenet newsgroup comp.ai.neural-nets, 1997, ftp://ftp.sas.com/pub/neural/FAQ.html

[2] LeCun, Y.; Bottou, L.; Orr, G. B.; Müller, K.-R.: Efficient backprop, Neural Networks: Tricks of the Trade. Springer, pp. 9-50.