|
| | FullyConnected (OutputInfo info, int J, bool bias, ActivationFunction act, double stdDev, Regularization regularization) |
| |
| virtual OutputInfo | initialize (std::vector< double * > ¶meterPointers, std::vector< double * > ¶meterDerivativePointers) |
| | Fill in the parameter pointers and parameter derivative pointers. More...
|
| |
| virtual void | initializeParameters () |
| | Initialize the parameters. More...
|
| |
| virtual void | updatedParameters () |
| | Generate internal parameters from externally visible parameters. More...
|
| |
| virtual void | forwardPropagate (Eigen::MatrixXd *x, Eigen::MatrixXd *&y, bool dropout, double *error=0) |
| | Forward propagation in this layer. More...
|
| |
| virtual void | backpropagate (Eigen::MatrixXd *ein, Eigen::MatrixXd *&eout, bool backpropToPrevious) |
| | Backpropagation in this layer. More...
|
| |
| virtual Eigen::MatrixXd & | getOutput () |
| | Output after last forward propagation. More...
|
| |
| virtual Eigen::VectorXd | getParameters () |
| | Get the current values of parameters (weights, biases, ...). More...
|
| |
| virtual | ~Layer () |
| |
Fully connected layer.
Each neuron in the previous layer is taken as input for each neuron of this layer. Forward propagation is usually done by 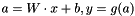 , where
, where 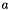 is the activation vector,
is the activation vector, 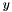 is the output,
is the output, 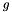 a typically nonlinear activation function that operates on a vector,
a typically nonlinear activation function that operates on a vector, 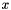 is the input of the layer,
is the input of the layer, 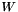 is a weight matrix and
is a weight matrix and 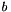 is a bias vector.
is a bias vector.
Actually, we have a faster implementation that computes the forward and backward pass for N instances in parallel. Suppose we have an input matrix 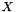 with
with 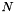 rows and
rows and 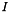 columns, i.e. each row contains an input vector
columns, i.e. each row contains an input vector 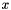 . The forward propagation is implemented in two steps:
. The forward propagation is implemented in two steps:
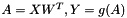
and the backpropagation is
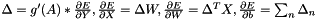
Neural networks with one fully connected hidden layer and a nonlinear activation function are universal function approximators, i. e. with a sufficient number of nodes any function can be approximated with arbitrary precision. However, in practice the number of nodes could be very large and overfitting is a problem. Therefore it is sometimes better to add more hidden layers. Note that this could cause another problem: the gradients vanish in the lower layers such that these cannot be trained properly. If you want to apply a complex neural network to tasks like image recognition you could instead try Convolutional layers and pooling layers (MaxPooling, Subsampling) in the lower layers. These can be trained surprisingly well in deep architectures.
Supports the following regularization types:
- L1 penalty
- L2 penalty
- Maximum of squared norm of the incoming weight vector
[1] Kurt Hornik, Maxwell B. Stinchcombe and Halbert White: Multilayer feedforward networks are universal approximators, Neural Networks 2 (5), pp. 359-366, 1989.

 Inheritance diagram for OpenANN::FullyConnected:
Inheritance diagram for OpenANN::FullyConnected: Public Member Functions inherited from OpenANN::Layer
Public Member Functions inherited from OpenANN::Layer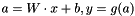 , where
, where 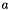 is the activation vector,
is the activation vector, 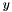 is the output,
is the output, 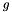 a typically nonlinear activation function that operates on a vector,
a typically nonlinear activation function that operates on a vector, 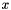 is the input of the layer,
is the input of the layer, 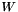 is a weight matrix and
is a weight matrix and 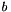 is a bias vector.
is a bias vector.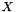 with
with 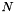 rows and
rows and 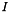 columns, i.e. each row contains an input vector
columns, i.e. each row contains an input vector 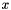 . The forward propagation is implemented in two steps:
. The forward propagation is implemented in two steps: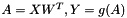
 1.8.4
1.8.4