Mini-batch stochastic gradient descent. More...

#include <MBSGD.h>

Inheritance diagram for OpenANN::MBSGD:

Public Member Functions
	MBSGD (double learningRate=0.01, double momentum=0.5, int batchSize=10, bool nesterov=false, double learningRateDecay=1.0, double minimalLearningRate=0.0, double momentumGain=0.0, double maximalMomentum=1.0, double minGain=1.0, double maxGain=1.0)
	Create mini-batch stochastic gradient descent optimizer. More...

	~MBSGD ()

virtual void	setOptimizable (Optimizable &opt)
	Pass the objective function. More...

virtual void	setStopCriteria (const StoppingCriteria &stop)
	Pass the stop criteria. More...

virtual void	optimize ()
	Optimize until the optimization meets the stop criteria. More...

virtual bool	step ()
	Execute one optimization step. More...

virtual Eigen::VectorXd	result ()
	Determine the best result. More...

virtual std::string	name ()
	Get the name of the optimization algorithm. More...

Public Member Functions inherited from OpenANN::Optimizer
virtual	~Optimizer ()

Detailed Description

Mini-batch stochastic gradient descent.

This implementation of gradient descent has some modifications:

it is stochastic, we update the weights with a randomly chosen subset of the training set to escape local minima and thus increase the generalization capabilities
we use a momentum to smooth the search direction
each weight has an adaptive learning rate
we can decrease the learning rate during optimization
we can increase the momentum during optimization

A good introduction to optimization with MBSGD can be found in Geoff Hinton's Coursera course "Neural Networks for Machine Learning". A detailed description of this implementation follows.

When the batch size equals 1, the algorithms degenerates to stochastic gradient descent. When it equals the training set size, the algorithm is like batch gradient descent.

Standard mini-batch stochastic gradient descent updates the weight vector w in step t through

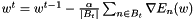
$w^t = w^{t-1} - \frac{\alpha}{|B_t|} \sum_{n \in B_t} \nabla E_n(w)$

or

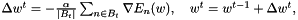
$\Delta w^t = - \frac{\alpha}{|B_t|} \sum_{n \in B_t} \nabla E_n(w), \quad w^t = w^{t-1} + \Delta w^t,$

where 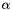$\alpha$ is the learning rate and 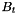$ B_t $ is the set of indices of the t-th mini-batch, which is drawn randomly. The random order of gradients prevents us from getting stuck in local minima. This is an advantage over batch gradient descent. However, we must not make the batch size too small. A bigger batch size makes the optimization more robust against noise of the training set. A reasonable batch size is between 10 and 100. The learning rate has to be within [0, 1). High learning rates can result in divergence, i.e. the error increases. Too low learning rates might make learning too slow, i.e. the number of epochs required to find an optimum might be infeasibe. A reasonable value for :math:\\alpha is usually within [1e-5, 0.1].

A momentum can increase the optimization stability. In this case, the update rule is

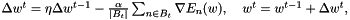
$\Delta w^t = \eta \Delta w^{t-1} - \frac{\alpha}{|B_t|} \sum_{n \in B_t} \nabla E_n(w), \quad w^t = w^{t-1} + \Delta w^t,$

where 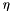$\eta$ is called momentum and must lie in [0, 1). The momentum term incorporates past gradients with exponentially decaying influence. This reduces changes of the search direction. An intuitive explanation of this update rule is: we regard w as the position of a ball that is rolling down a hill. The gradient represents its acceleration and the acceleration modifies its momentum.

Another type of momentum that is available in this implementation is the Nesterov's accelerated gradient (NAG). For smooth convex functions, NAG achieves a convergence rate of 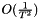$O(\frac{1}{T^2})$ instead of 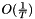$O(\frac{1}{T})$ [1]. The update rule only differs in where we calculate the gradient.

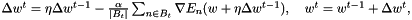
$\Delta w^t = \eta \Delta w^{t-1} - \frac{\alpha}{|B_t|} \sum_{n \in B_t} \nabla E_n(w + \eta \Delta w^{t-1}), \quad w^t = w^{t-1} + \Delta w^t,$

Another trick is using different learning rates for each weight. For each weight 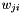$w_{ji}$ we can introduce a gain 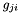$g_{ji}$ which will be multiplied with the learning rate so that we obtain an update rule for each weight

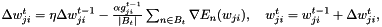
$\Delta w_{ji}^t = \eta \Delta w_{ji}^{t-1} - \frac{\alpha g_{ji}^{t-1}}{|B_t|} \sum_{n \in B_t} \nabla E_n(w_{ji}), \quad w_{ji}^t = w_{ji}^{t-1} + \Delta w_{ji}^t,$

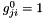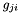where $g_{ji}^0 = 1$ and $g_{ji}$ will be increased by 0.05 if 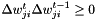$\Delta w_{ji}^t \Delta w_{ji}^{t-1} \geq 0$ , i.e. the sign of the search direction did not change and 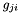$g_{ji}$ will be multiplied by 0.95 otherwise. We set a minimum and a maximum value for each gain. Usually these are 0.1 and 10 or 0.001 and 100 respectively.

During optimization it often makes sense to start with a more global search, i.e. with a high learning rate and decrease the learning rate as we approach the minimum so that we obtain an update rule for the learning rate:

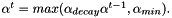
$\alpha^t = max(\alpha_{decay} \alpha^{t-1}, \alpha_{min}).$

In addition, we can allow the optimizer to change the search direction more often at the beginning of the optimization and reduce this possibility at the end. To do this, we can start with a low momentum and increase it over time until we reach a maximum:

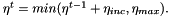
$\eta^t = min(\eta^{t-1} + \eta_{inc}, \eta_{max}).$

[1] Sutskever, Ilya; Martens, James; Dahl, George; Hinton, Geoffrey: On the importance of initialization and momentum in deep learning, International Conference on Machine Learning, 2013.

Constructor & Destructor Documentation

OpenANN::MBSGD::MBSGD	(	double	learningRate = `0.01`,
		double	momentum = `0.5`,
		int	batchSize = `10`,
		bool	nesterov = `false`,
		double	learningRateDecay = `1.0`,
		double	minimalLearningRate = `0.0`,
		double	momentumGain = `0.0`,
		double	maximalMomentum = `1.0`,
		double	minGain = `1.0`,
		double	maxGain = `1.0`
	)

Create mini-batch stochastic gradient descent optimizer.

Parameters

learningRate	learning rate (usually called alpha); range: (0, 1]
momentum	momentum coefficient (usually called eta); range: [0, 1)
batchSize	size of the mini-batches; range: [1, N], where N is the size of the training set
nesterov	use nesterov's accelerated momentum
learningRateDecay	will be multiplied with the learning rate after each weight update; range: (0, 1]
minimalLearningRate	minimum value for the learning rate; range: [0, 1]
momentumGain	will be added to the momentum after each weight update; range: [0, 1)
maximalMomentum	maximum value for the momentum; range [0, 1]
minGain	minimum factor for individual learning rates
maxGain	maximum factor for individual learning rates