Two Spirals

Data Set

This is a classification benchmark which is particularly difficult for gradient descent optimization.

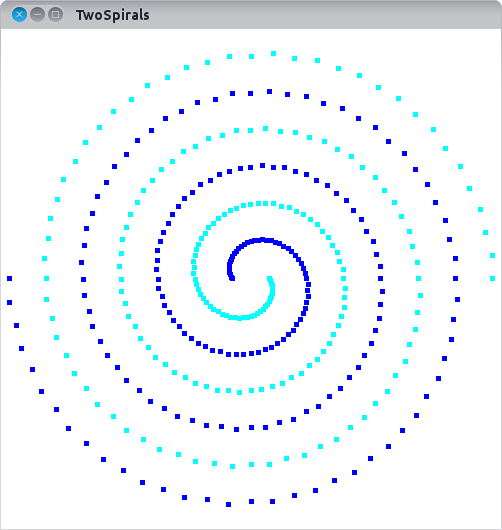
The two spirals data set was developed by Lang and Witbrock [1]. The data set we use here is taken from the CMU Neural Networks Benchmarks. It consists of 193 training instances and 193 test instances located on a 2D surface. They belong to one of two spirals:

Network Architecture

It is possible to solve this problem with one or two hidden layers. But architectures with two hidden layers need less connections and can learn faster. The architecture we chose here is 2-20-20-1 with bias. You can solve this problem with different compression setups. the smallest number of parameters that reliably solves this problem is 3-6-1 with orthogonal cosine functions. All activation functions are tangens hyperbolicus (MLP::TANH). The best optimization algorithm is Levenberq-Marquardt (MLP::BATCH_LMA).

User Interface

You can use the following keys to control the program:

• Q: Toggle display of training set
• W: Toggle display of test set
• E: Toggle display of predicted classes for the whole surface
• R: Toggle display of smooth prediction transitions (black+white or grey)
• A: Start visible training
• Escape: Quit application.

A trained model could make these predictions:

References

[1] Kevin J. Lang and Michael J. Witbrock: Learning to Tell Two Spirals Apart. In: Proceedings of the 1988 Connectionist Models Summer School,

1. ISBN: 0-55860-015-9

Code

Note that you should not use this as an example for good GUI code because it mixes a lot of logic and visualization.

#include "TwoSpiralsVisualization.h"
#include <QApplication>
#include <OpenANN/OpenANN>
#include "CreateTwoSpiralsDataSet.h"
#ifdef PARALLEL_CORES
#include <omp.h>
#endif

int main(int argc, char** argv)
{
  useAllCores(); // Enable all cores (must be specified during build)
  OpenANNLibraryInfo::print();
  QApplication app(argc, argv);

  Eigen::MatrixXd Xtr, Ytr, Xte, Yte;
  createTwoSpiralsDataSet(2, 1.0, Xtr, Ytr, Xte, Yte);
  TwoSpiralsVisualization visual(Xtr, Ytr, Xte, Yte);
  visual.show();
  visual.resize(500, 500);

  return app.exec();
}

#ifndef TWO_SPIRALS_VISUALIZATION_H_
#define TWO_SPIRALS_VISUALIZATION_H_

#include <OpenANN/OpenANN>
#include <OpenANN/io/DirectStorageDataSet.h>
#include <Eigen/Core>
#include <QGLWidget>
#include <QKeyEvent>
#include <QMutex>

using namespace OpenANN;

class TwoSpiralsVisualization;

class TwoSpiralsDataSet : public DataSet
{
  Eigen::MatrixXd in, out;
  DirectStorageDataSet dataSet;
  TwoSpiralsVisualization* visualization;
public:
  TwoSpiralsDataSet(const Eigen::MatrixXd& inputs, const Eigen::MatrixXd& outputs);
  void setVisualization(TwoSpiralsVisualization* visualization);
  virtual ~TwoSpiralsDataSet() {}
  virtual int samples() { return dataSet.samples(); }
  virtual int inputs() { return dataSet.inputs(); }
  virtual int outputs() { return dataSet.outputs(); }
  virtual Eigen::VectorXd& getInstance(int i) { return dataSet.getInstance(i); }
  virtual Eigen::VectorXd& getTarget(int i) { return dataSet.getTarget(i); }
  virtual void finishIteration(Learner& learner);
};

class TwoSpiralsVisualization : public QGLWidget
{
  Q_OBJECT
  int width, height;
  QMutex classesMutex;
  double classes[100][100];
  TwoSpiralsDataSet trainingSet;
  TwoSpiralsDataSet testSet;
  bool showTraining, showTest, showPrediction, showSmooth;
  Net* net;
  StoppingCriteria stop;

public:
  TwoSpiralsVisualization(const Eigen::MatrixXd& trainingInput, const Eigen::MatrixXd& trainingOutput,
                          const Eigen::MatrixXd& testInput, const Eigen::MatrixXd& testOutput);
  virtual ~TwoSpiralsVisualization();
  void predictClass(int x, int y, double predictedClass);

protected:
  virtual void initializeGL();
  virtual void resizeGL(int width, int height);
  virtual void paintGL();
  void paintPrediction();
  void paintDataSet(bool training);
  virtual void keyPressEvent(QKeyEvent* keyEvent);

signals:
  void updatedData();
};

#endif // TWO_SPIRALS_VISUALIZATION_H_

#include "TwoSpiralsVisualization.h"
#include <OpenANN/util/AssertionMacros.h>
#include <GL/glu.h>
#include <QApplication>

TwoSpiralsVisualization::TwoSpiralsVisualization(
  const Eigen::MatrixXd& trainingInput,
  const Eigen::MatrixXd& trainingOutput,
  const Eigen::MatrixXd& testInput,
  const Eigen::MatrixXd& testOutput)
  : width(500), height(500),
    trainingSet(trainingInput, trainingOutput),
    testSet(testInput, testOutput), showTraining(true), showTest(true),
    showPrediction(true), showSmooth(true), net(new Net)
{
  std::memset(classes, 0, sizeof(double) * 100 * 100);
  trainingSet.setVisualization(this);
  QObject::connect(this, SIGNAL(updatedData()), this, SLOT(repaint()));

  // initialize MLP
  net->inputLayer(trainingSet.inputs())
  // use this as only hidden layer to try extreme learning machine
  //.extremeLayer(1500, RECTIFIER, 1.0)
  .fullyConnectedLayer(20, TANH)
  .fullyConnectedLayer(20, TANH)
  .outputLayer(trainingSet.outputs(), TANH)
  .trainingSet(trainingSet);
  net->initialize();

  // set stop criteria
  stop.maximalIterations = 10000;
  stop.minimalSearchSpaceStep = 1e-8;
  stop.minimalValueDifferences = 1e-8;
}

TwoSpiralsVisualization::~TwoSpiralsVisualization()
{
  delete net;
}

void TwoSpiralsVisualization::predictClass(int x, int y, double predictedClass)
{
  classesMutex.lock();
  classes[x][y] = predictedClass;
  classesMutex.unlock();
  if(x == 99 && y == 99)
    emit updatedData();
}

void TwoSpiralsVisualization::initializeGL()
{
  glEnable(GL_DEPTH_TEST);
  glEnable(GL_LINE_SMOOTH);
  glHint(GL_LINE_SMOOTH_HINT, GL_NICEST);
  glEnable(GL_BLEND);
  glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
  glDepthFunc(GL_LEQUAL);
  glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);
  glShadeModel(GL_SMOOTH);
  glClearColor(0.0, 0.0, 0.0, 0.0);
  glPointSize(5.0);
}

void TwoSpiralsVisualization::resizeGL(int width, int height)
{
  this->width = width;
  this->height = height;
  glViewport(0, 0, width, height);
  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluPerspective(45.0f, (float) width / (float) height, 1.0f, 100.0f);
  glMatrixMode(GL_MODELVIEW);
  glClearColor(0.0, 0.0, 0.0, 0.0);
  glClearDepth(1.0f);
}

void TwoSpiralsVisualization::paintGL()
{
  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
  glLoadIdentity();
  glTranslatef(-0.5f, -0.5f, -1.25f);

  if(showPrediction)
    paintPrediction();

  if(showTraining)
    paintDataSet(true);

  if(showTest)
    paintDataSet(false);

  glFlush();
}

void TwoSpiralsVisualization::paintPrediction()
{
  for(int x = 0; x < 100; x++)
  {
    for(int y = 0; y < 100; y++)
    {
      classesMutex.lock();
      float c;
      Eigen::VectorXd v(2);
      v(0) = (double) x / 100.0f;
      v(1) = (double) y / 100.0f;
      if(showSmooth)
        c = classes[x][y] / 2.0f + 0.5f;
      else
        c = classes[x][y] < 0.0 ? 0.0f : 1.0f;
      classesMutex.unlock();
      glColor3f(c, c, c);
      float minX = (float) x / 100.0f - 0.005;
      float maxX = minX + 0.01;
      float minY = (float) y / 100.0f - 0.005;
      float maxY = minY + 0.01;
      glBegin(GL_QUADS);
      glVertex2f(minX, maxY);
      glVertex2f(maxX, maxY);
      glVertex2f(maxX, minY);
      glVertex2f(minX, minY);
      glEnd();
    }
  }
}

void TwoSpiralsVisualization::paintDataSet(bool training)
{
  TwoSpiralsDataSet& dataSet = training ? trainingSet : testSet;
  glBegin(GL_POINTS);
  for(int n = 0; n < dataSet.samples(); n++)
  {
    if(dataSet.getTarget(n)(0) > 0.0)
      glColor3f(1.0f, 0.0f, 0.0f);
    else
      glColor3f(1.0f, 1.0f, 0.0f);
    glVertex2d(dataSet.getInstance(n)(0), dataSet.getInstance(n)(1));
  }
  glEnd();
}

void TwoSpiralsVisualization::keyPressEvent(QKeyEvent* keyEvent)
{
  switch(keyEvent->key())
  {
  case Qt::Key_Q:
    OPENANN_INFO << "Switching training set on/off.";
    showTraining = !showTraining;
    update();
    break;
  case Qt::Key_W:
    OPENANN_INFO << "Switching test set on/off.";
    showTest = !showTest;
    update();
    break;
  case Qt::Key_E:
    OPENANN_INFO << "Switching prediction on/off.";
    showPrediction = !showPrediction;
    update();
    break;
  case Qt::Key_R:
    OPENANN_INFO << "Switching smooth classes on/off.";
    showSmooth = !showSmooth;
    update();
    break;
  case Qt::Key_A:
    OPENANN_INFO << "Training with restart (" << net->dimension() << " parameters)...";
    train(*net, "LMA", MSE, stop, true);
    break;
  case Qt::Key_Escape:
    OPENANN_INFO << "Quitting application.";
    QApplication::quit();
    break;
  default:
    QGLWidget::keyPressEvent(keyEvent);
    break;
  }
}

TwoSpiralsDataSet::TwoSpiralsDataSet(const Eigen::MatrixXd& inputs, const Eigen::MatrixXd& outputs)
  : in(inputs), out(outputs), dataSet(&this->in, &this->out), visualization(0)
{
}

void TwoSpiralsDataSet::setVisualization(TwoSpiralsVisualization* visualization)
{
  this->visualization = visualization;
}

void TwoSpiralsDataSet::finishIteration(Learner& learner)
{
  if(visualization)
  {
    for(int x = 0; x < 100; x++)
    {
      for(int y = 0; y < 100; y++)
      {
        Eigen::VectorXd in(2);
        in << (double) x / 100.0, (double) y / 100.0;
        Eigen::VectorXd out = learner(in);
        visualization->predictClass(x, y, out(0, 0));
      }
    }
  }
}